Models Beyond the Standard Model

Up to now, we have seen that a quantum field theory with quarks, leptons and vector bosons for three different forces describes reasonably well all the experimental data available so far. Among the vector bosons, however, those corresponding to the weak force (which is responsible for the β-decay of nucleons) are known to have masses. There are three such vector bosons, and they are called W+, W− and Z bosons, or weak bosons, as a whole. From the consistency of quantum field theories, it is known that something must be behind the nonzero masses of these vector bosons.

What is called the Standard Model provides a simple theoretical idea how the weak bosons acquire masses. According to the Standard Model, the masses originate from condensation of quanta of a new scalar boson, called Higgs boson. The Higgs boson was the last missing piece of the Standard Model, and was discovered in LHC experiments in 2012. The observed mass about 125 GeV is consistent with the mechanism predicted by the Standard Model. This mass is also consistent with our prediction in supersymmetric standard model with relatively large SUSY breaking at 10-100 TeV.

Is that the end of the story? No, definitely not. Let us think about the following questions.

  • The Higgs boson is the only scalar field in the Standard Model; all other dynamical degrees of freedom in the Standard Model are either fermions or vector fields. Why does the Standard Model have one scalar field, and just one? Why does its condensation develop?
  • The Newton constant GN≃ 6.7×10−11 m3kg/s2corresponds to an energy scale 1/ GNℏ/c3〜 1019GeV. Why is there a huge hierarchy of order 1017between this energy scale and the weak boson masses of order 102GeV, and how can the weak boson masses remain so small under quantum corrections?

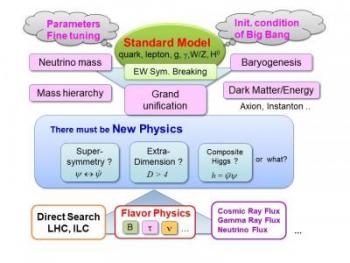
In order to solve these questions theoretically, various models beyond the Standard Model have been constructed so far, and we still continue to do so in quest of a better solution to these problems. Once we have concrete models, we can examine whether such models are really consistent with all the available experimental data, predict what kind of signals can be expected in future experiments, and even propose experiments to confirm such models.

The origin of the masses of the weak bosons is not the only puzzle of the Standard Model. It is known that huge fraction of the universe consists of dark matter and dark energy. It is very unlikely that dark matter is actually the ordinary matter particles in the Standard Model.

This is where we find another motivation to extend the Standard Model. Our universe may have become so large because of an inflationary process in the early universe, and quantum fluctuations of a scalar field may become the fluctuations of density in the early universe, which eventually become galaxies and clusters of galaxies. So, here is another motivation to introduce a new degree of freedom and extend the Standard Model. Such cosmological issues as inflation, primordial density perturbations and dark matter motivate extensions of the Standard Model, and models in quantum field theories are the appropriate framework in order to work on these issues.

Recent reports of excess in high-energy cosmic ray fluxes, deviation from the Standard-Model prediction of the anomalous magnetic moment of muon, and some other reports of deviations from the Standard Model predictions may also be indications of some physics beyond the Standard Model. We therefore seek for theoretical models that account for these phenomena.

We also address the following problems. The Standard Model is described by a quantum field theory with about 30 parameters, and the values of these parameters can be determined only by measuring them experimentally. Would it be possible to determine them theoretically, by considering theoretical frameworks that contain the Standard Model?

The thermal history of early universe is described very well by the Standard Model at least back to the era with the temperature of order MeV, but it is only with several input parameter values of initial condition of the universe. Those initial condition parameters include baryon asymmetry, normalization of density contrast and the amount of dark energy. How are these initial condition parameters set? Once again, it is impossible to think about such problems without a model that extends the Standard Model. Kavli IPMU researchers are intensively pursuing to discover and understand new physics beyond the SM from various aspects, as mentioned in other research programs. (Last update: 2018/05/07)

Members