Quantum field theory (QFT) is, as the name suggests, the study of quantum properties of fields, where the word "fields" means whatever physical entities extending along the space and the time. Such extended physical entities include the electromagnetic wave and the oscillation of crystals, and are ubiquitous in our world. Therefore quantum field theory is basic to many parts of the theoretical physics, for example in high-energy particle physics and condensed matter physics. Indeed its study was initiated about a hundred years ago, soon after the quantum mechanics itself was developed.
In one sense, quantum field theory is by now well-developed and has been applied to many phenomena, and the results of computations in quantum field theory are known to reproduce experimental results accurately. For example, the Standard Model of particle physics itself, which describes the interactions of elementary particles below the energy scale currently accessible to us, is one particular quantum field theory among others. Not only that, there are many subjects in mathematics developed partly by various types of inspirations coming from the study of quantum field theory, such as the Seiberg-Witten theory of four-dimensional manifolds.
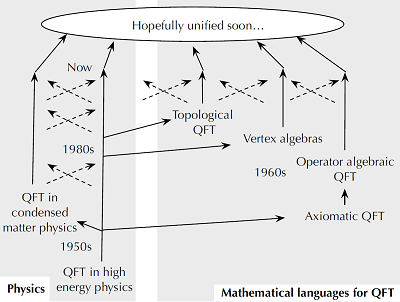
Still, quantum field theory is a young, immature and developing field of theoretical physics. One indication of its relative youth is that there has not been any agreed-upon mathematical language which can express what physicists do with quantum field theory, although mathematicians did try to formulate various parts of it in the past. This is in stark contrast to the situation with e.g. quantum mechanics and general relativity, for which we have precise mathematical theories. It is true that physicists do know a set of rules which allows them to compute experimentally-observed quantities, but the framework encompassing these rules is still beyond reach.
A number of researchers in Kavli IPMU are involved in advancing our understanding of quantum field theory, and this activity transcends the traditional subdivision within physics and mathematics. It is a research area where condensed matter physicists, string theorists, particle phenomenologists and mathematicians can equally make contributions.
Some samples of the works of these researchers are:
- A systematic method to compute the number of possible operators in any effective field theory, including the Standard Model. This is such a fundamental piece of information about any quantum field theory, but before this work it was done by hand in an ad hoc manner which was error-prone.
- A re-analysis of the quantum anomaly of finite symmetries such as Zn. Again this particular case was previously obtained using an embedding into continuous U(1) symmetry, but with a new method which originated in condensed matter theory and which became available in the last few years, it can now be determined from the first principle.
- A precise mathematical formulation of the concept of the "Coulomb branch", the part of the supersymmetric moduli space of a three-dimensional N=4 supersymmetric quantum field theory. Mathematically this amounts to an association of a holomorphic symplectic variety to a pair of a group and its representation, which is different to and morally dual to the construction known as the hyperkahler reduction.
(Last update: 2018/09/07)