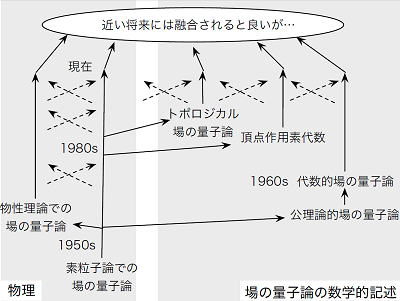
場の量子論は、名の示す通り、場を量子的に調べる理論です。
空間方向と時間方向に広がっていれば物理的なものは何でも場と呼ばれますので、たとえば電磁波も、結晶の振動も、場の例です。ですから、場の量子論は、理論物理の広い局面で基本となる分野で、素粒子理論においても物性理論においても重要です。そのため、その研究はほぼ百年前、量子力学自体が建設されてすぐの時代に始まっています。
現在では、ある意味においては、場の量子論は充分に確立しており、いろいろな物理現象に適用され、計算結果は実験結果を広く正確に再現します。現在到達可能なエネルギースケールにおける素粒子の相互作用を記述する所謂標準模型も、そのような場の量子論の一例です。それだけでなく、数学のいろいろな分野が、場の量子論からのアイデアをもとに築かれています。四次元多様体のザイバーグ・ウィッテン理論がその例としてあげられます。
しかし、別の観点からは、場の量子論は理論物理としてまだまだ未熟で発展中です。量子力学ならばヒルベルト空間の上の作用素の理論、一般相対性理論ならばローレンツ多様体上のアインシュタイン方程式の理論があります。しかし、場の量子論に対しては、数学者がこれまでいろいろな定式化をしなかったわけではありませんが、物理屋が現在場の量子論と称して行う計算を表現し得る枠組みはいまだ数学にはありません。場の量子論は、実験結果と比較すべき数値を計算する一連のルールを提供こそしますが、それを束ねる枠組みを欠いているわけです。
Kavli IPMU の研究者には、このような場の量子論の理解の現状を改善すべく努力している人達がいます。この仕事は、物理や数学のなかの伝統的な分野わけを越えた活動と言うことができ、実際、物性物理屋も、素粒子現象論屋も、弦理論屋も、純粋数学者も、一緒になって研究を行っています。
これらの研究者の過去の研究結果をいくつか挙げておきましょう:
- 標準模型を含む一般的な有効場の理論にどのような演算子があるかを系統的に調べる方法の開発。この情報は、どのような場の理論においても非常に基本的なものですが、これまでは間違いやすいその場限りの方法で行われてきました。
- Zn 有限対称性の量子異常の再導出。この現象も、以前に連続対称性である U(1) に埋め込むことによって計算はされていましたが、近年物性物理から導入された新手法をもちいると、直接第一原理的に計算することが出来ます。
- 「クーロン枝」の正則シンプレクティック多様体としての厳密な数学的定義。この「クーロン枝」は、三次元 N=4 超対称量子場の理論の真空のモジュライ空間の一部ですが、数学的には、群とその表現の組に対して、既存のハイパーケーラー商構成とは異なる、ある意味双対な方法で多様体を定義せよということになります。
(Last update: 2018/09/07)
メンバー
- Sunjin Choi
- Tomohiro Fujita
- Vaibhav Gautam
- Yannis Georis
- Andrei Grekov
- Anamaria Hell
- Sagharsadat Hosseinisemnani
- Yiwen Huang
- Ryuichiro Kitano
- Qiuyue Liang
- Luca Marchetti
- Thomas (Tom) Melia
- Yuan Miao
- Hiraku Nakajima
- Jiaxin Qiao
- Jie Sheng
- Yuji Tachikawa
- Masataka Watanabe
- Vicharit Yingcharoenrat
- Hao Zhang
- Mengyang Zhang
- Yi Zhang






